202207181946 Category Theory in Life

Category theory is abstract, but its abstraction makes it apply to many things around us in ordinary life.

What is category theory?

Category theory is the mathematics of mathematics

Mathematics is the logical study of how logical things work.

In order to study things logically, we have to ignore some details of reality that make things behave illogically. It's only in the abstract world where things do behave perfectly logically

Category theory is the logical theory study of the logical study of how logical things work.

The map of the London underground is a good example of a "mathematics", where the geographical map of the exact tubes are not the purpose. The slightly unreal, more representative version helps us in a certain situation navigate more easily. We choose to ignore certain details to represent things more logically.

Objects and morphisms

$A \rightarrow B$ means there's a $morphism$ between $A$ and $B$.

So if we have

$$A \xrightarrow{\text{is the mother of}} B \xrightarrow{\text{is the mother of}} C$$

We can deduce

$$A \xrightarrow{\text{is the grandmother of}} C$$

Instead of looking at things based on their intrinsic characteristics, we can learn a lot about them (and other things) by their relationships to other things: hence the "Category". This gives us more context

It would be weird if you wrote a biography about someone but didn't write at all about their relationships with other people or things. It wouldn't be much of a biography at all. We exist in relation to other things.

One of the core keys to category theory is composition. Composition means we can travel along multiple arrows (e.g. in the example above) that can be deduced, and then leave out all the arrows that can be deduced. In the above, $A \rightarrow B \rightarrow C \Rightarrow A \rightarrow C$.

A category consists of

• some objects $A$, $B$, and $C$
• some morphisms (arrows) $A \rightarrow B$
• composition and identities
• associativity and unit laws

Associativity allows association order of implications of single arrow chains.

$$A \rightarrow B \rightarrow C \rightarrow D$$

Can be

$$A \rightarrow C \Rightarrow A \rightarrow D$$

or

$$B \rightarrow D \Rightarrow A \rightarrow D$$

The grandmother of my mother is the mother of my grandmother.

Commutative squares are common in category theory and people use these all the time whether they know it or not.

        A -- brother --> B
        |                |
husband |                | wife
        |                |
        V                V
        C -- sister  --> D

What's the diagonal? Brother-in-law via spouse is usually not the same as your brother-in-law via your sibling.

Factors of 30 are ${1, 2, 3, 5, 6, 10, 15, 30}$, but there's more interesting information here if we draw these in 2D in relation to which ones are factors of others. These make a cube because of their prime factors and their multiplication.

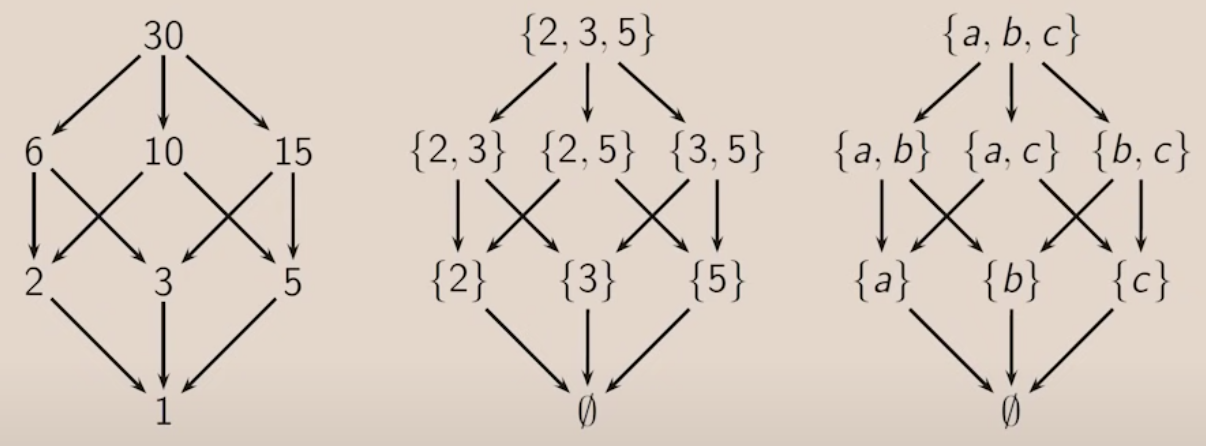
Which is a category of partially ordered set of all subsets of 3 things.

Excellent segment on white privilege and a skewed cuboid that's analogous to that factor example.

The principle of sameness

Are the equations truly equal on a meta level?

$$ 8 + 1 = 1 + 8 $$

$$ 2 x 5 = 5 x 2 $$

Not necessarily. It's easier to calculate $8 + 1$ for most people than $8 + 1$. It could be easier to carry two 5 pound things than five 2 pound things.

But even if $8 + 1$ is easier, $8 + (5 + 5)$ is easier than $(8 + 5) + 5$ because of base 10 and how that works out. Therefore,

All equations are lies... or useless

The only equation that is not a lie is $x = x$

Adding sugar to eggs, then adding milk and heating, we get custard. If we add milk and sugar, then add eggs and heat it up, we don't get custard. For a cake though, it doesn't really matter. We can mostly just throw it all in the bowl and get nearly the same thing. We get to choose whether associativity is "sameness". Choosing which things are the same is the same as defining invertibility.

Invertibility morphism is the ability to go somewhere and come back to the same place.

$$1 + 4 = 5 \rightarrow 5 - 4 = 1$$

but

$$-3^2 = 9 \not\rightarrow \sqrt{9} \not= -3$$

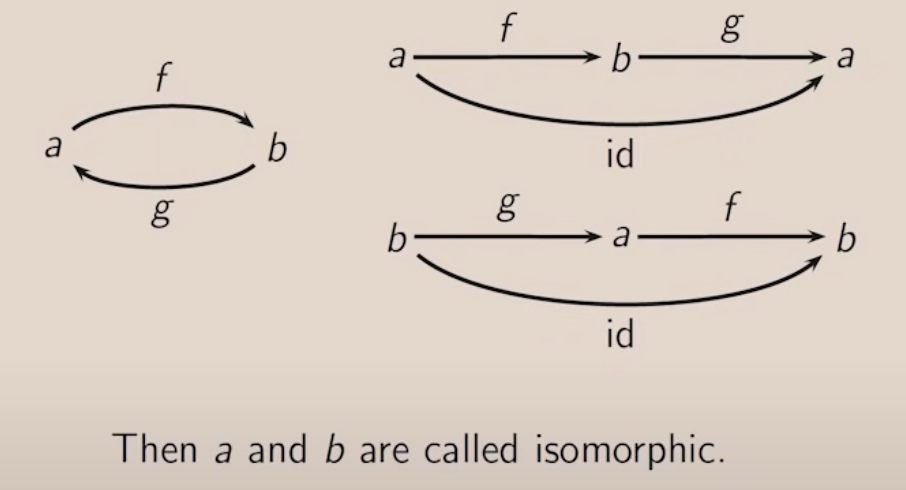
Isomorphic objects are treated the same by the rest of the category. Things can be isomorphic in one category but not another.

Whole categories can be isomorphic.

Equality doesn't mean men and women are the same — it is about when the world should treat them the same.

Universal Properties

Characterizing things by the role they play in that context

This is a really relevant piece about software engineering.

An initial object in a category is an object $I$ such that for all objects $X$ there is a unique morphism $I \rightarrow X$. In the factors of 30 example. The "top" 30 is the initial object, or the "top" ${a,b,c}$ subset.

Something not universal can be universal in another.

Visual Representation

Can highlight things yes, but more for engaging and enhancing our intuition about these abstract things that we don't interact with regularly in the real world.

Can analyze things that happened in the world and visualize the interconnectedness of what lead to that happening. This is similar to systems thinking but in a less "stocks and flows" way and more of causal chains.

Lessons from category theory

• Everything should be understood in context
• Everyone is privileged in some contexts and not in others
• Everything should be studied in relationship with other things, not in isolation.

Abstraction takes us further from "reality"...

...but casts a wider light on it.

Wider light is dimmer, but illuminates more than bright narrow light. We need to shine the light closely sometimes too, but also pull back.

Category Theory in Life